数据特征分析- 统计分析指标有哪些??

字数统计: 811阅读时长: 4 min

 2019/12/19 

可进行分析的类别:

集中趋势度量: `一组数据向某一中心靠拢的倾向`

数值平均数

算数平均值(pd.series.mean()):

>> data = pd.DataFrame({'value':np.random.randint(100,120,4),'f':np.random.rand(4)})
>> print(data)
index	value	f
0	113	0.30
1	102	0.20
2	102	0.32
3	106	0.1

>> desc = data.describe()
>> print(desc)

label\feature   	value	f	
count	4	4
mean	105.75	0.2475
std	5.18813	0.0736546
min	102	0.17
25%	102	0.1925
50%	104	0.25
75%	107.75	0.305
max	113	0.32

几何平均值/a开n次方(stats.gmean):

>> desc.loc['gmean'] = data.apply(gmean)  # 使用scipy.stats.geman 函数
>> desc.loc['man-gmean'] = data.apply(lambda x: pow(pd.DataFrame.prod(x), 1.0/4)) # 使用自定义函数实现
>> print(desc)

label\feature   	value	f	
gmean	105.656	0.239022
man-gmean	105.656	0.239022

位置平均数

中位数(pd.series.median):

>> desc.loc['median'] = data.apply(pd.Series.median)
>> print(desc)

label\feature   	value	f	
median	104	0.25

众数(pd.series.mode):

1
2
3

>> desc.loc['mode'] = data.apply(lambda x: ",".join((x.astype('str').mode().tolist())))
label\feature   	value	f	
mode	102.0	0.17,0.2,0.3,0.32

密度曲线(kde)

fig = plt.figure()
fig.set(alpha=0.2)  # 设定图表颜色alpha参数
 
plt.subplot2grid((2,4),(0,0)) 
data['value'].plot(kind='kde',style='--k',grid=True, figsize=(10,6))

相关曲线

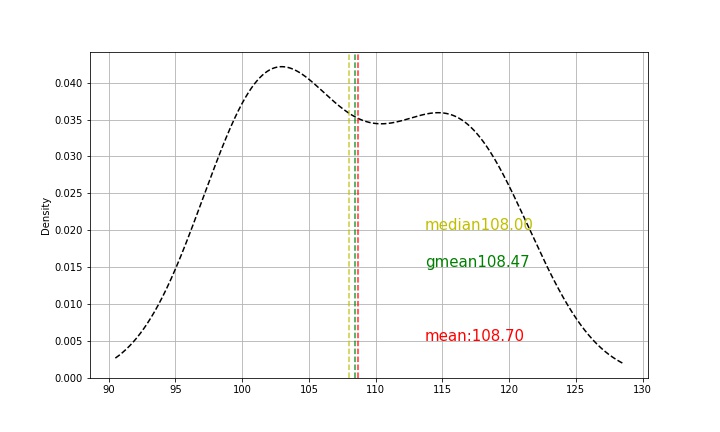
离中趋势度量(标志变动度): `一组数据中各数据值以不同程度偏离其中心(平均数)的趋势`

极差: 没有考虑中间值的变动情况，测定离中趋势时不准确 最大-最小

>> desc.loc['range'] = data.apply(lambda x: x.max() - x.min())

label\feature   	value	f	
range	19	0.17

四分位差: 75% - 25%

>> desc.loc['quantile'] = desc.loc['75%'] - desc.loc['25%']

label\feature   	value	f	
quantile	14	0.0575

标准差: (pd.series.std)

>> desc.loc['man-std'] = data.apply(pd.Series.std)

label\feature   	value	f	
man-std	5.18813	0.0736546

样本方差:

desc.loc['sample_var'] = data.apply(pd.Series.var)
desc.loc['man-sample-var'] = data.apply(lambda x: (pow(x-x.mean(),2).sum())/(len(data['value'])-1)) # 使用自定义函数实现

label\feature   	value	f	
sample_var	26.9167	0.005425
man-sample-var	26.9167	0.005425

总体方差:


def calEx(data):
    """
    求总体期望
    data: df['feature'].value_counts()
    """
    
    f = pd.DataFrame({'index':data.value_counts().index, 'value':data.value_counts()},columns=['index','value'])
    f['value_rate'] = f['value']/f['value'].sum()
    ex = (f['value_rate']* f['index']).sum()
    return ex
desc.loc['all_var'] = data.apply(pd.Series.var)
desc.loc['man-all-val'] = data.apply(lambda x: pow((pow(x-calEx(x),2).sum())/(len(data['value'])),1.0/2)) # 使用自定义函数实现

label\feature   	value	f	
all_var	4.49305	0.0637868
man-all-val	4.49305	0.0637868